龙驭球《结构力学Ⅰ》第二章课后习题详解
2-1 试分析图2-2-1所示体系的几何构造。
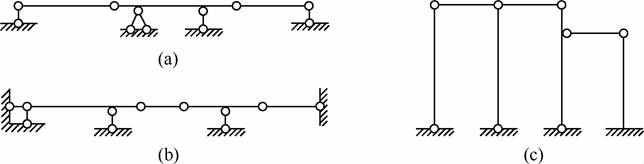
图2-2-1
解:(1)如图2-2-2所示,ABC和DEF为两个二元体,可以撤除,剩下的杆CD通过不共点的三链杆与基础相连,形成几何不变体,二元体不影响原结构的几何不变性,故体系为几何不变体系,且无多余约束。

图2-2-2
(2)如图2-2-3所示,刚片AB通过不共点三链杆1、2、3与基础相连,形成几何不变体。将刚片AB和基础视为新的基础,刚片CD通过链杆BC、DE及链杆4与基础相连,但是这三链杆交于同一点,即链杆4与刚片CD的交点,故体系为有一个多余约束的瞬变体系。
注:瞬变体系必定有多余约束。

图2-2-3
(3)如图2-2-4所示,ABC和DCE为二元体,将其撤除,视刚片HI与地基固结为一个基础,刚片EG、FH通过不共线的三个铰G、F、H与基础相连,形成几何不变体,二元体不影响原结构的几何不变性,所以该体系为几何不变体系,且无多余约束。
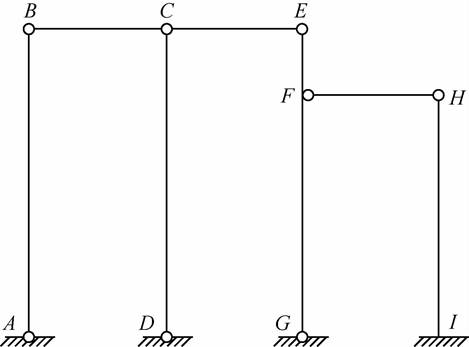
图2-2-4
2-2 试分析图2-2-5所示体系的几何构造。
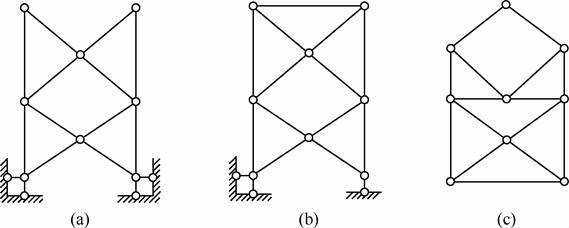
图2-2-5
解:(1)如图2-2-6(a)所示,将刚片1和2、刚片3和4、刚片5和6、刚片7和8、刚片9和10、刚片11和12视为二元体,将其依次撤除,只剩下大地基础,故体系为几何不变体系,且无多余约束。
(2)如图2-2-6(b)所示,去掉杆1,剩下的杆件依次可判断为二元体:2和10、3和12、4和5、6和11、7和13、8和9,去掉二元体后,结构缺一个水平横向约束成为无多余约束的几何不变体系,加上杆1,结构为无多余约束的几何不变体系。
(3)如图2-2-6(c)所示,下部由基本三角形Ⅰ、Ⅱ和Ⅲ组成,为几何不变体系,可视为一个大的刚片,上部依次拆除二元体1和2、3和4、5和6,刚片7和8与下部大的刚片通过共线的三铰相连,形成瞬变体,故体系为有一个多余约束的瞬变体系。
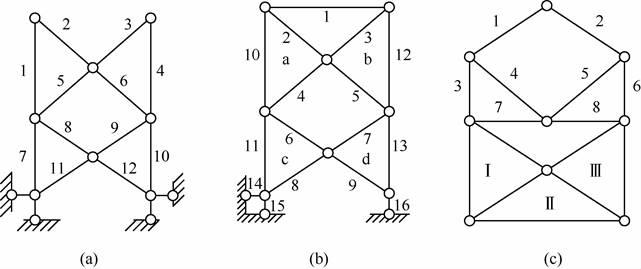
图2-2-6
2-3 试分析图2-2-7所示体系的几何构造。
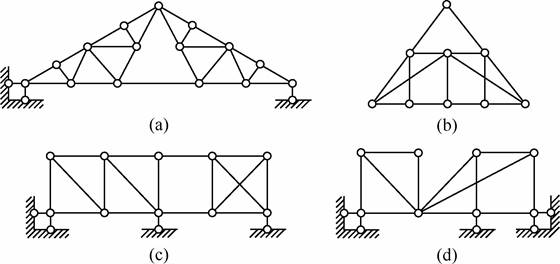
图2-2-7
解:(1)如图2-2-8(a)所示,△ABC是通过基本三角形和增加二元体形成的,是一个几何不变体,视为一个刚片,同理,△ADE也可视为一个刚片,刚片ABC、ADE通过不共线的三铰A、C、D与刚片CD连在一起形成一个几何不变体△ABE,而整个上部△ABE结构与基础通过不平行且不相交于一点的三链杆与支座相连,故体系为几何不变体系,且无多余约束。
(2)如图2-2-8(b)所示,视基本三角形GHE为一刚片,则追加二元体HD和DE、CD和CG、则可视GCDEH为一大刚片,同理左侧的基本三角形ABF和二元体GA和GF形成一个大的刚片,这两个大刚片通过不在同一直线上的铰G、B、C与刚片BC相连,形成几何不变体,再加上上部的二元体IF和IH,故整体为几何不变体系,且无多余约束。
(3)如图2-2-8(c)所示,ABCFED为基本三角形和二元体组成,与基础通过不相互平行且不相交于一点的三链杆相连,可一起视为刚片Ⅰ,GHKJ为基本△HGK和二元体GJH组成几何不变体,且多一约束HJ,视为刚片Ⅱ,则两刚片通过不平行且不交于一点的链杆CG、FJ和K处下部链杆相连,故体系为几何不变体系,且有一多余约束。
(4)如图2-2-8(d)所示,左部分ABDC由基本三角形和二元体组成,视为刚片Ⅰ,右侧刚片DEF,并依次追加二元体DGE、GHF,一起视为刚片Ⅱ,则刚片Ⅰ和Ⅱ与基础通过共线的三铰D、C、H相连,图示三个铰共线了,根据三刚片规则,即为没有多余约束的瞬变体系;多了一个横向约束,故体系为有一个多余约束的几何不变体系。
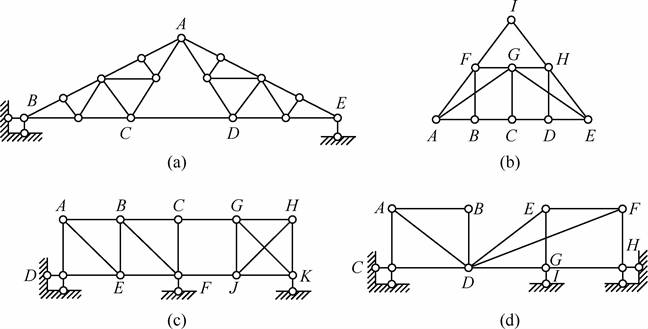
图2-2-8
2-4 试分析图2-2-9所示体系的几何构造。

图2-2-9
解:(1)如图2-2-10(a)所示,视链杆AB、BC和DE分别为刚片Ⅰ、Ⅱ和Ⅲ,则三刚片由实铰B和虚铰O′、O相连,若O′、O和B不在一条直线上,则体系为几何不变体系,且无多余约束,反之则为有一个多余约束的几何瞬变体系。
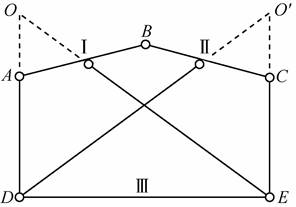
图2-2-10(a)
(2)如图2-2-10(b)所示,分别视基本△ABC和△CDE为刚片Ⅰ和Ⅱ,视链杆FG为刚片Ⅲ,则刚片Ⅰ和Ⅱ通过铰C相连,刚片Ⅰ和Ⅲ通过交于E点的链杆AG和BF相连,相当于一个瞬铰在E点。同理,刚片Ⅱ和Ⅲ通过交于A点的链杆GE和DF相连,相当于一个瞬铰在A点,则三刚片通过不共线的三铰相连,故体系为几何不变体系,且无多余约束。

图2-2-10(b)
(3)如图2-2-10(c)所示,分别视AEB和BFC为刚片Ⅰ和Ⅱ,视基础为刚片Ⅲ,则刚片Ⅰ和Ⅱ通过铰B相连,刚片Ⅰ和Ⅲ通过链杆AD和铰E处的链杆形成的瞬铰O相连,刚片Ⅱ和Ⅲ通过链杆CG和铰F处的链杆形成的瞬铰O′相连,则三刚片由不共线的三铰O、O′、B相连,故体系为几何不变体系,且无多余约束。
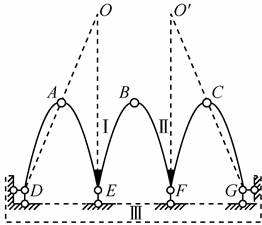
图2-2-10(c)
(4)如图2-2-10(d)所示,视三角形AEC和链杆BD为刚片Ⅰ和Ⅱ,视基础为刚片Ⅲ,则刚片Ⅰ和Ⅱ通过无穷远的瞬铰O12相连,刚片Ⅱ和Ⅲ通过无穷远的瞬铰O23相连,刚片Ⅰ和Ⅲ通过实铰E相连,则三刚片通过一个实铰E和不同方向的两无穷远的瞬铰相连,故体系为几何不变体系,且无多余约束。

图2-2-10(d)
(5)如图2-2-10(e)所示,由基本三角形组成的刚片ABDC与基础通过不共线且不交于一点的三链杆相连组成了不变体系,追加二元体ED和E处基础链杆,仍为不变体系,则视它们一起为刚片Ⅰ,视由基本三角形组成的FGHK为刚片Ⅱ,则两刚片由交于G点的三链杆BF、EH和K处链杆相连,故体系为有一个多余约束的瞬变体系。

图2-2-10(e)
| 内容来源 |
龙驭球《结构力学Ⅰ》第4版教材考点笔记课后答案 |
扫码阅读 |
2-5 试分析图2-2-11所示体系的几何构造。
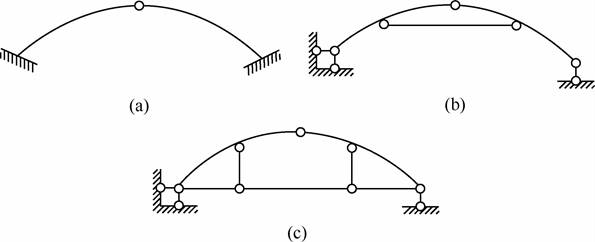
图2-2-11
解:(1)如图2-2-12(a)所示,去掉中间的铰C,则两边体系均为几何不变体系,铰C为多余的两个约束,故整个体系为几何不变体系,有两个多余约束。

图2-2-12(a)
(2)如图2-2-12(b)所示,整个上部结构与基础通过不平行且不相交于一点的三链杆支座相连,故可以直接考虑上部结构的几何特性,刚片AB、BC和DE通过不共线的三铰B、D、E相连,故体系为几何不变体系,且无多余约束。
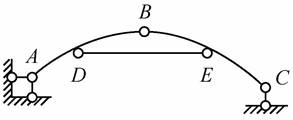
图2-2-12(b)
(3)如图2-2-12(c)所示,同图(b)可知,只需考虑除基础的结构,刚片AB、BD和DC通过不共线的三铰D、B、C相连,则ABDC可视为刚片Ⅰ,同理AFGE视为刚片Ⅱ,则两刚片通过不共线的三铰A、D、G和刚片DG相连,故组成不变体系,所以体系为几何不变体系,且无多余约束。
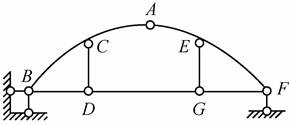
图2-2-12(c)
2-6 试分析图2-2-13所示体系的几何构造。

图2-2-13
解:(1)如图2-2-14(a)所示,依次拆除二元体EDF、BAC,只剩下基础,故体系为几何不变体系,且无多余约束。
(2)如图2-2-14(b)所示,刚片AB、BCD和基础通过不共线的三铰B、A、D两两相连,构成几何不变体,再加上右边的二元体CEF,故体系为几何不变体系,且无多余约束。
(3)如图2-2-14(c)所示,刚片BCE通过交于一点O的三链杆AB、CD和EF与基础相连,故体系为有一个多余约束的瞬变体系。
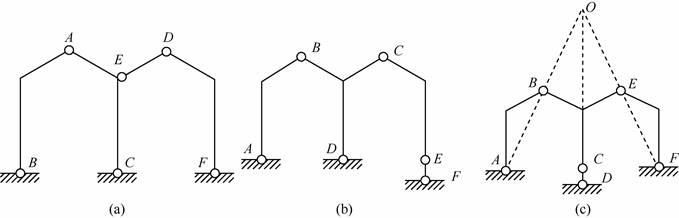
图2-2-14
2-7 试分析图2-2-15所示体系的几何构造。
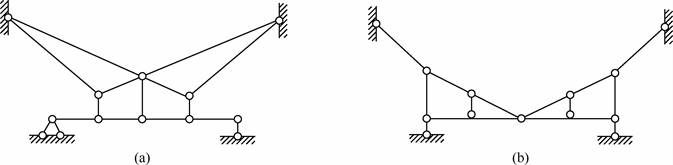
图2-2-15
解:(1)如图2-2-16(a)所示,刚片ABD、刚片CBE和基础通过不共线的三铰A、B、C相连,构成几何不变体,再加上不影响几何结构不变性的二元体IKM、EIH、BHG、DGF,则体系为几何不变体系,且无多余约束。
(2)如图2-2-16(b)所示,易知ABC和CDE均为几何不变体,视刚片ABC和CDE分别为Ⅰ和Ⅱ,视基础为刚片Ⅲ,则三刚片通过不共线的实铰C和瞬铰A、E相连,故体系为几何不变体系,且无多余约束。
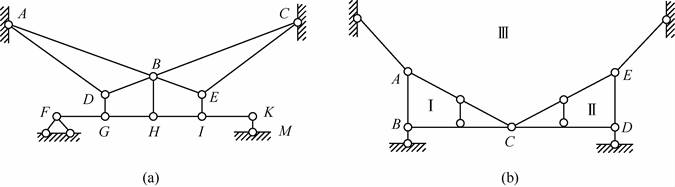
图2-2-16
2-8 试分析图2-2-17所示体系的几何构造。
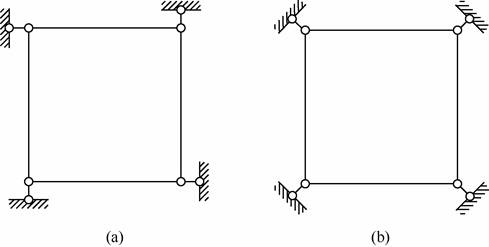
图2-2-17
解:(1)如图2-2-18(a)所示,视链杆AB和CD分别为刚片1和2,基础为刚片3,则三刚片通过不共线的瞬铰B、D和无穷远处的瞬铰相连,故体系为几何不变体系,且无多余约束。
(2)如图2-2-18(b)所示,视链杆AB和CD为刚片1和2,基础为刚片3,则三刚片通过相交于一点的瞬铰O和无穷远处的瞬铰相连,故体系为有一个多余约束的瞬变体系。
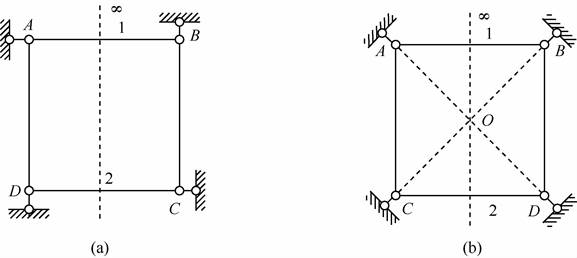
图2-2-18
2-9 试分析图2-2-19所示体系的几何构造。

图2-2-19
解:(1)如图2-2-20(a)所示,视由基本三角形组成的ABD和BCE为刚片1和2,基础为刚片3,则1和2刚片通过铰B相连,1和3刚片通过瞬铰O1相连,2和3刚片通过瞬铰O2相连。三刚片通过不共线的三铰B、O1、O2相连,故体系为几何不变体系,且无多余约束。
(2)如图2-2-20(b)所示,刚片ABD和BCE通过铰B相连,刚片ABD与基础通过交于A点的二链杆相连,刚片BCE与基础通过交于C点的二链杆相连,点A、B和C共线,故体系为有一个多余约束的瞬变体系。
(3)如图2-2-20(c)所示,将链杆CD视为刚片,刚片BEF与刚片CD通过交于点O1的二链杆BC、DE相连,刚片BEF与基础通过交于F的链杆AB、F处的支座链杆相连,刚片CD与基础通过交于点O2的二链杆相连,三瞬铰O1、O2和F不共线,故体系为几何不变体系,且无多余约束。

图2-2-20
完整版链接: http://dacai.100xuexi.com/Ebook/996439.html
【目录】达聪学习网“龙驭球《结构力学Ⅰ》第4版复习笔记课后答案”
第1章 绪 论
1.1 复习笔记
1.2 课后习题详解
1.3 名校考研真题详解
第2章 结构的几何构造分析
2.1 复习笔记
2.2 课后习题详解
2.3 名校考研真题详解
第3章 静定结构的受力分析
3.1 复习笔记
3.2 课后习题详解
3.3 名校考研真题详解
第4章 影响线
4.1 复习笔记
4.2 课后习题详解
4.3 名校考研真题详解
第5章 静定结构位移计算的虚力法
5.1 复习笔记
5.2 课后习题详解
5.3 名校考研真题详解
第6章 力 法
6.1 复习笔记
6.2 课后习题详解
6.3 名校考研真题详解
第7章 位移法
7.1 复习笔记
7.2 课后习题详解
7.3 名校考研真题详解
第8章 渐近法及其他算法简述
8.1 复习笔记
8.2 课后习题详解
8.3 名校考研真题详解
第9章 静定结构总论
9.1 复习笔记
9.2 课后习题详解
9.3 名校考研真题详解
第10章 超静定结构总论
10.1 复习笔记
10.2 课后习题详解
10.3 名校考研真题详解
热门文章
——————————————————————————————
· 银行从业资格《法律法规与综合能力》中级考试必做1200题







