同济大学数学系《高等数学》第7版课后习题答案详解 【完整内容点击文中链接获取】
第1章 函数与极限
1、求下列函数的自然定义域:
(1)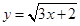 ;(2)y=1/(1-x2);
;(2)y=1/(1-x2);
(3) ;(4)
;(4)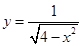 ;
;
(5)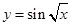 ;(6)y=tan(x+1);
;(6)y=tan(x+1);
(7)y=arcsin(x-3);(8)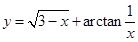 ;
;
(9)y=ln(x+1);(10)y=e1/x。
解:(1)3x+2≥0⇒x≥-2/3,故其定义域为[-2/3,+∞)。
(2)1-x2≠0⇒x≠±1,故其定义域为(-∞,-1)∪(-1,1)∪(1,+∞)。
(3)x≠0且1-x2≥0⇒x≠0且|x|≤1,故其定义域为[-1,0)∪(0,1]。
(4)4-x2>0⇒|x|<2,故其定义域为(-2,2)。
(5)x≥0,故其定义域为[0,+∞)。
(6)x+1≠kπ+π/2(k∈Z),故其定义域为{x|x∈R且x≠(k+1/2)π-1,k∈Z}。
(7)|x-3|≤1⇒2≤x≤4,故其定义域为[2,4]。
(8)3-x≥0且x≠0,故其定义域为(-∞,0)∪(0,3]。
(9)x+1>0⇒x>-1,故其定义域为(-1,+∞)。
(10)x≠0,故其定义域为(-∞,0)∪(0,+∞)。
2、下列各题中,函数f(x)和g(x)是否相同?为什么?
(1)f(x)=lgx2,g(x)=2lgx;
(2)f(x)=x,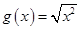 ;
;
(3)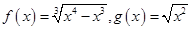 ;
;
(4)f(x)=1,g(x)=sec2x-tan2x。
解:(1)函数f(x)和g(x)不同,因其定义域不同。
(2)函数f(x)和g(x)不同,因其对应法则不同,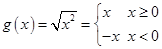
(3)函数f(x)和g(x)相同,因其定义域、对应法则均相同。
(4)函数f(x)和g(x)不同,因其定义域不同。
3、设
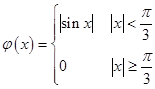
求φ(π/6),φ(π/4),φ(-π/4),φ(-2),并作出函数y=φ(x)的图形。
解:
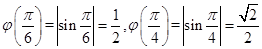
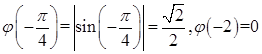
y=φ(x)的图形如图1-2-1所示。
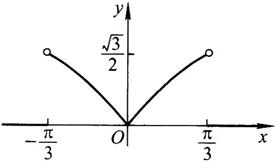
图1-2-1
| 内容来源 |
同济大学《高等数学》(第7版)笔记和课后答案  |
4、试证下列函数在指定区间内的单调性:
(1)y=x/(1-x),(-∞,1);
(2)y=x+lnx,(0,+∞)。
证:(1)y=x/(1-x)=-1+1/(1-x),(-∞,1)。
设x1<x2<1,因为
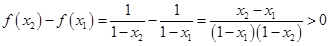
所以f(x2)>f(x1),即f(x)在(-∞,1)内单调增加。
(2)设0<x1<x2,因为f(x2)-f(x1)=x2+lnx2-x1-lnx1=x2-x1+ln(x2/x1)>0,可得f(x2)>f(x1),所以f(x)在(0,+∞)内单调增加。
5、设f(x)为定义在(-l,l)内的奇函数,若f(x)在(0,l)内单调增加,证明f(x)在(-l,0)内也单调增加。
证:设-l<x1<x2<0,则0<-x2<-x1<l,因为f(x)是奇函数,所以f(x2)-f(x1)=-f(-x2)+f(-x1),又因为f(x)在(0,1)内单调增加,所以f(-x1)-f(-x2)>0,从而f(x2)>f(x1),即f(x)在(-l,0)内也单调增加。
6、设下面所考虑的函数都是定义在区间(-l,l)上的。证明:
(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数;
(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数。
证:(1)设f1(x),f2(x)均为偶函数,则f1(-x)=f1(x),f2(-x)=f2(x)。
令F(x)=f1(x)+f2(x),于是F(-x)=f1(-x)+f2(-x)=f1(x)+f2(x)=F(x),故F(x)为偶函数。
设g1(x),g2(x)均为奇函数,则g1(-x)=-g1(x),g2(-x)=-g2(x),令G(x)=g1(x)+g2(x),于是G(-x)=g1(-x)+g2(-x)=-g1(x)-g2(x)=-G(x),故G(x)为奇函数。
(2)设f1(x),f2(x)均为偶函数,则f1(-x)=f1(x),f2(-x)=f2(x),令F(x)=f1(x)·f2(x),于是F(-x)=f1(-x)·f2(-x)=f1(x)f2(x)=F(x),故F(x)为偶函数。
设g1(x),g2(x)均为奇函数,则g1(-x)=-g1(x),g2(-x)=-g2(x),令G(x)=g1(x)·g2(x),于是G(-x)=g1(-x)·g2(-x)=[-g1(x)][-g2(x)]=g1(x)g2(x)=G(x),
故G(x)为偶函数。
设f(x)为偶函数,g(x)为奇函数,则f(-x)=f(x),g(-x)=-g(x),令H(x)=f(x)·g(x),于是H(-x)=f(-x)·g(-x)=f(x)[-g(x)]=-f(x)·g(x)=-H(x),故H(x)为奇函数。
……
【完整版】 达聪网 同济大学数学系《高等数学》(第7版)笔记和课后习题(含考研真题)详解
热门内容
[电子书]同济大学数学系《高等数学》(第7版)(上册)配套题库【考研真题精选+章节题库】
[电子书]同济大学数学系《高等数学》(第7版)(下册)配套题库【考研真题精选+章节题库】
同济大学数学系《高等数学》(第7版)(上册)精讲视频【教材精讲+考研真题串讲】







