计量经济学基础古扎拉蒂第五版答案

[大] [中] [小] 发布人：达聪学习网发布日期：2022-04-12 共405人浏览过

古扎拉蒂《计量经济学基础》（第5版）课后习题详解

本书参考了大量计量经济学相关资料对该教材的课（章）后习题进行了详细的分析和解答，并对相关重要知识点进行了延伸和归纳。
立即阅读 >>

古扎拉蒂《计量经济学基础》（第5版）课后习题答案详解【完整内容点击文中链接获取】

第8章多元回归分析：推断问题

1 假如你要研究某产品，比如说汽车，在某些年里的销售情况，有人建议你试用下面的模型：

Y_t＝β₀＋β₁t

Y_t＝α₀＋α₁t＋α₂t²

其中Y_t＝时间t的销售量，t＝时间（以年计）。第一个模型假设销售量是时间的线性函数，而第二个模型把它表述为时间的二次函数。

a．讨论这些模型的性质。

b．你会如何在两个模型之间做出选择？

c．在什么情况下二次模型是有用的？

d．试图找到美国在过去20年里的汽车销售量数据，并看哪个模型对数据拟合的较好。

答：a．在第一个模型中，销售量是时间的线性函数，于是销售量随时间的变化率（dY/dt）就是一个等于β₁的常数，与时间t无关。在第二个模型中，由于dY/dt＝α₁＋2α₂t，所以销售变化率就不是一个常数，而是与时间t有关。

b．最简单的办法就是将Y对时间描点。如果得到的散点图看起来像抛物线，可能二次模型比较合适。

c．用这个模型描述一个人的收入经历或许比较恰当。很明显，当一个人刚进入劳动市场时，他的收入较低，随着经验的积累，收入也不断增加，但过了一定的年龄之后，收入便开始下降。

d．从几家汽车制造厂的网站、汽车杂志或美国汽车联合会搜寻数据。

2证明方程（8.4.16）中的F比率等于方程（8.4.18）中的F比率。（提示：ESS/TSS＝R²。）

证明：因为F＝[（ESS_new－ESS_old）/NR]/[RSS_new/（n－k）]，其中，NR＝新回归元的个数。将分子和分母同时除以TSS，并根据R²＝ESS/TSS和1－R²＝RSS/TSS，代入方程F＝[（ESS_new－ESS_old）/NR]/[RSS_new/（n－k）]便得到方程（8.4.18）。

3证明方程（8.4.18）和（8.6.10）中的F检验是等价的。

证明：这是一个定义上的问题，如教材中提到的，无约束回归被称为长回归或新回归，而受约束回归则被称为短回归。二者的差别在于模型中所包含的回归元个数。

内容来源

古扎拉蒂《计量经济学基础》（第5版）课后习题详解

4证明命题（8.6.11）和（8.6.12）。

证明：在OLS估计中，在不对估计量做任何限制的情况下最小化RSS。因此，此时的RSS代表了真正最小的RSS或RSS_UR。在对一个或多个参数施加约束时，由于施加了限制，可能得不到绝对最小的RSS。于是，除非所施加的限制完全正确，此时这两个RSS项将相同，否则便有RSS_R＞RSS_UR。因为R²＝1－RSS/TSS，于是R_UR²＝1－RSS_UR/TSS≥R_R²＝1－RSS_R/TSS。

无论是否施加限制，TSS都是相同的，都等于：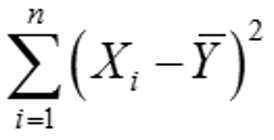

5考虑柯布-道格拉斯生产函数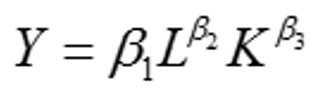：（1）

其中Y＝产出，L＝劳动力投入，K＝资本投入。把方程（1）的两边同时除以K得到：（2）

取（2）的自然对数得：ln（Y/K）＝β₀＋β₂ln（L/K）＋（β₂＋β₃－1）lnK＋u_i（3），其中β₀＝lnβ₁。

a．假如你有做回归（3）的数据，你会怎样检验规模报酬不变即β₂＋β₃＝1这个假设？

b．如果有规模报酬不变情形，你会怎样解释回归（3）？

c．用L而不用K去除方程（1），会有什么不同吗？

答：a．令logK的系数为β^*＝β₂＋β₃－1。利用通常的t检验，检验虚拟假设β^*＝0。若确实存在规模报酬不变，则t值会很小。

b．如果定义Y/K为产出资本比（对资本生产力的一种度量），L/K为劳动资本比，那么，这个回归中的斜率系数的含义是，劳动资本比变化1个百分点，导致资本生产力的平均百分比变化。

c．即使这种分析是对称的，假定规模报酬不变，此时的斜率系数表示，资本劳动比变化1个百分点，导致劳动生产力平均变化多少个百分点。发达国家与发展中国家的区别是：发达国家一般都具有更高的资本劳动比。

6当R²＝0时的R²临界值。方程（8.4.11）给出在全部偏斜率系数同时为零（即R²＝0）的假设下F与R²的关系。正如我们能从F表求出在显著性水平α上的F临界值，我们能通过以下关系式求出R²临界值：R²＝[（k－1）F]/[（k－1）F＋（n－k）]。其中k是回归模型中包括截距在内的参数个数，而F是在显著性水平α上的F临界值。如果所测的R²超过从上述公式计算出来的临界R²值，就可拒绝真实R²为零的假设。证明上述公式并求出（在α＝5%处）回归（8.1.4）的R²临界值。