材料力学刘鸿文第6版课后答案

[大] [中] [小] 发布人：达聪学习网发布日期：2022-05-03 共820人浏览过

（1）梳理知识脉络，浓缩学科精华。本书每章的复习笔记均对该章的重难点进行了整理，并参考了国内名校名师讲授该教材的课堂笔记。因此，本书的内容几乎浓缩了该教材的知识精华。
（2）详解课后习题，巩固重点难点。本书参考大量相关辅导资料，对刘鸿文主编的《材料力学》（第6版）的课后思考题进行了详细的分析和解答，并对相关重要知识点进行了延伸和归纳。
（3）精编考研真题，培养解题思路。本书精选详析了部分名校近年来的相关考研真题，这些高校均以该教材作为考研参考书目。所选考研真题基本涵盖了每章的考点和难点，考生可以据此了解考研真题的命题风格和难易程度，并检验自己的复习效果。
立即阅读 >>

刘鸿文《材料力学》（第6版）笔记和课后习题（含考研真题）详解【完整内容点击文中链接获取】

1.2 课后习题详解

1.1 对图1-2-1所示钻床，试求n-n截面上的内力。

图1-2-1

解：应用截面法，沿n-n截面将钻床分成两部分，取n-n截面右半部分进行受力分析，如图1-2-2所示。

由平衡条件可得

∑Fy＝0，F－FS＝0

∑MC＝0，Fb－M＝0

则n-n截面内力为：FS＝F，M＝Fb。

图1-2-2

1.2 试求图1-2-3所示结构m-m和n-n两截面上的内力，并指出AB和BC两杆的变形属于何类基本变形。

图1-2-3

解：（1）应用截面法，取n-n截面以下部分进行受力分析，如图1-2-4（a）所示。

由平衡条件可得：∑MA＝0，FN×3－3×2＝0；

则截面内为：FN＝2kN（受拉）；

BC杆属于拉伸变形。

（2）应用截面法，取m-m截面右侧部分及n-n截面以下部分进行受力分析，如图1-2-4（b）所示。

由平衡条件可得

∑MO＝0，FN×2－3×1－M＝0

∑Fy＝0，FS＋FN－3＝0

则截面内为：FS＝1kN，M＝1kN·m。

AB杆属于弯曲变形。

图1-2-4（a）

图1-2-4（b）

内容来源：

刘鸿文《材料力学》（第6版）笔记和课后习题（含考研真题）详解

扫码在手机上做题

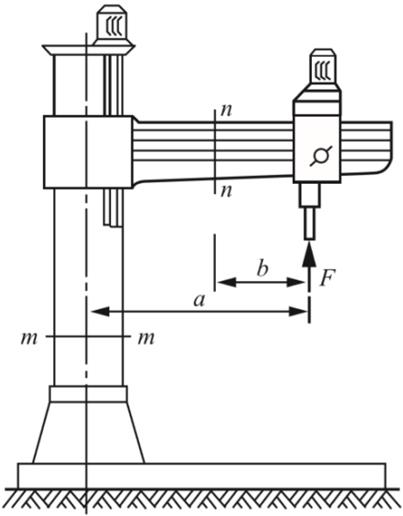
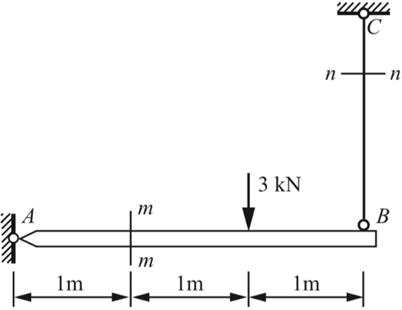
1.3 在图1-2-5所示简易吊车的横梁上，F力可以左右移动。试求截面1-1和2-2上的内力及其最大值。

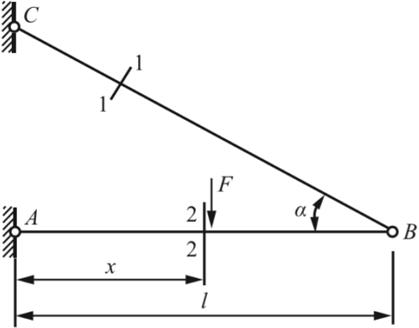
图1-2-5
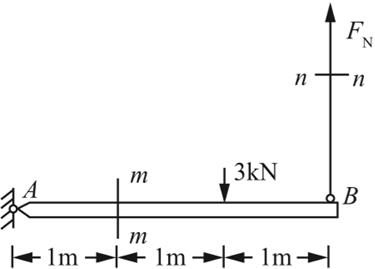
解：（1）应用截面法，取1-1截面以下部分进行受力分析，如图1-2-6（a）所示。
由平衡条件可得：∑MA＝0，FN1lsinα－Fx＝0；
解得：FN1＝Fx/（lsinα）；
故当x＝l时，1-1截面内力有最大值：FN1max＝F/sinα。
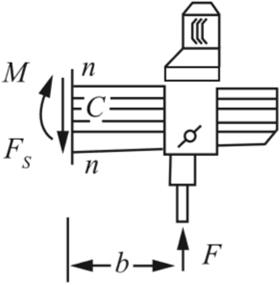
（2）应用截面法，取1-1截面以下，2-2截面右侧部分进行受力分析，如图1-2-6（b）所示。
由平衡条件可得
∑Fx＝0，FN2－FN1cosα＝0
∑Fy＝0，FS2－FN1sinα－F＝0
∑MO＝0，FN1（l－x）sinα－M2＝0
解得2-2截面内力：FN2＝Fxcotα/l，FS2＝（1－x/l）F，M2＝xF（l－x）/l。
综上可知，当x＝l时，FN2有最大值，且FN2max＝Fcotα；当x＝0时，FS2有最大值，且FS2max＝F；当x＝l/2时，弯矩M2有最大值，且M2max＝Fl/4。

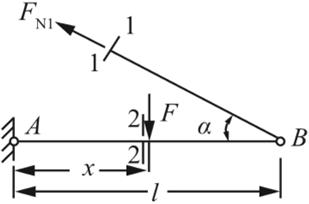
图1-2-6（a）

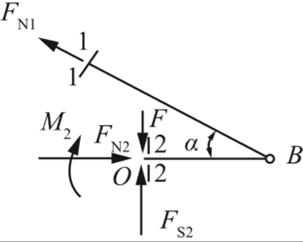
图1-2-6（b）
1.4 图1-2-7所示拉伸试样上A，B两点的距离l称为标距。受拉力作用后，用引伸计量出两点距离的增量为Δl＝5×10－2mm。若l的原长为l＝100mm，试求A、B两点的平均应变εm。

图1-2-7
解：由线应变的定义可知，A、B两点的平均应变为
εm＝Δl/l＝5×10－2/100＝5×10－4
1.5 图1-2-8所示的三角形薄板因受外力作用而变形，角点B垂直向上的位移为0.03mm，但AB和BC仍保持为直线。试求沿OB的平均应变，并求薄板在B点处的切应变。

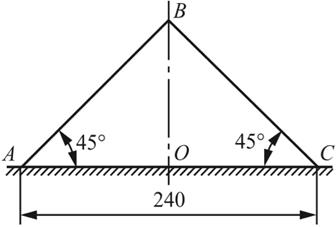
图1-2-8
解：如图1-2-9所示，由线应变的定义可知，沿OB方向的平均应变为
εm＝BB′/OB＝0.03/120＝2.5×10－4
变形后AB与BC两边的角度改变量为：π/2－∠AB′C＝γB。
γB非常微小，由图示几何关系有
γB＝π/2－2arctan[120/（120＋0.03）]＝2.5×10－4rad

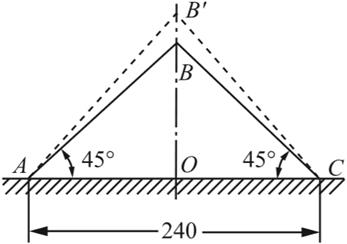
图1-2-9
……