同济大学数学系《工程数学—线性代数》(第6版)笔记和课后习题(含考研真题)详解 【完整内容点击文中链接获取】
第1章 行列式
1、利用对角线法则计算下列三阶行列式:
(1) ;
;
(2)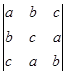 ;
;
(3)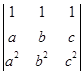 ;
;
(4)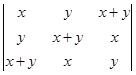 。
。
解:(1)原式=2×(-4)×3+0×(-1)×(-1)+1×1×8-1×(-4)×(-1)-2×(-1)×8-0×1×3=-4。
(2)原式=acb+bac+cba-c3-a3-b3=3abc-a3-b3-c3。
(3)原式=1·b·c2+1·c·a2+1·a·b2-1·b·a2-1·c·b2-1·a·c2=bc2+ca2+ab2-ba2-cb2-ac2=c2(b-a)+ab(b-a)-c(b2-a2)=(a-b)(b-c)(c-a)。
(4)原式=x(x+y)y+yx(x+y)+(x+y)yx-(x+y)3-x3-y3=-2(x3+y3)。
2、按自然数从小到大为标准次序,求下列各排列的逆序数:
(1)1 2 3 4;
(2)4 1 3 2;
(3)3 4 2 1;
(4)2 4 1 3;
(5)13…(2n-1)24…(2n);
(6)13…(2n-1)(2n)(2n-2)…2。
解:(1)该排列为标准排列,所以其逆序数为0。
(2)该排列的首位元素4的逆序数为0,第2位元素1的逆序数为1,第3位元素3的逆序数为1,末位元素2的逆序数为2,所以其逆序数为:0+1+1+2=4。
(3)该排列的前两位元素的逆序数均为0,第3位元素2的逆序数为2;末位元素1的逆序数为3,所以其逆序数为:0+0+2+3=5。
(4)该排列的从首位元素到末位元素的逆序数依次为0,0,2,1,所以其逆序数为:0+0+2+1=3。
(5)该排列中前n位元素的逆序数均为0,第n+1位元素2与它前面的n-1个数构成逆序对,所以它的逆序数为n-1;同理可知,第n+2位元素4的逆序数为n-2……末位元素2n的逆序数为0,因此该排列的逆序数为:(n-1)+(n-2)+…+0=n(n-1)/2。
(6)该排列的前n+1位元素的逆序数均为0;第n+2位元素(2n-2)的逆序数为2;第n+3位元素2n-4与它前面的2n-3,2n-1,2n,2n-2构成逆序对,所以它的逆序为4,……,末位元素2的逆序数为2(n-1),因此该排列的逆序数为:2+4+…+2(n-1)=n(n-1)。
3、写出四阶行列式中含有因子a11a23的项。
解:根据行列式的定义可知,此项必定还含有分别位于第3行和第4行的某两元素,而它们又分别位于第2列和第4列,即a32和a44或a34和a42,又因排列1324与1342的逆序数分别为1与2,所以,此行列式中含有a11a23的项为-a11a23a32a44与a11a23a34a42。
(1)
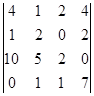 ;
;(2)
 ;
;(3)
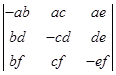 ;
;(4)
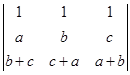 ;
;(5)
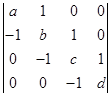 ;
;(6)
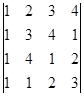 。
。解:(1)
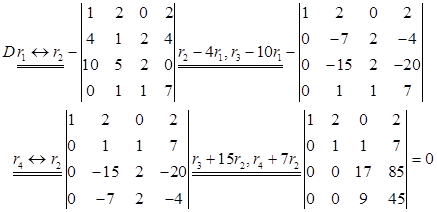
(2)
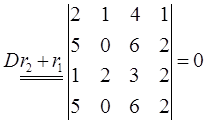
(3)
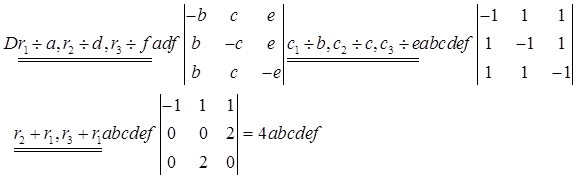
(4)
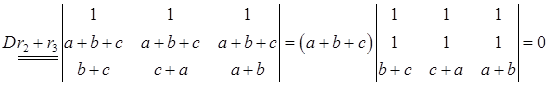
(5)
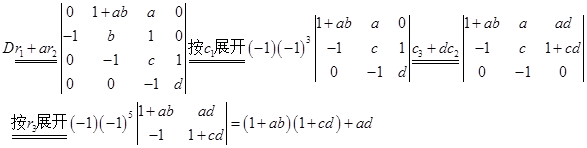
(6)
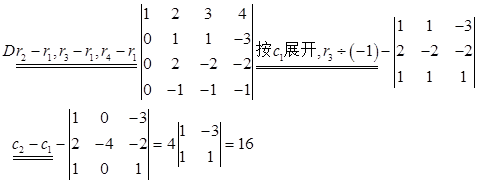
5、求解下列方程:
(1)
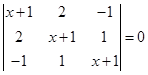 ;
;(2)
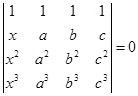 ,其中a,b,c互不相等。
,其中a,b,c互不相等。解:(1)
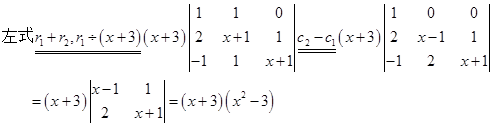
因此该方程的解为:
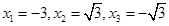 。
。(2)根据题意可知,方程左式为4阶范德蒙德行列式,则有
(x-a)(x-b)(x-c)(a-b)(a-c)(b-c)=0
又因为a,b,c互不相等,因此该方程的解为:x1=a,x2=b,x3=c。
……
【完整版】 达聪网 同济大学数学系《工程数学—线性代数》(第6版)笔记和课后习题(含考研真题)详解
热门内容
同济大学数学系《工程数学—线性代数》(第6版)配套题库【考研真题精选+章节题库】






