程守洙普通物理学第七版课后题答案

程守洙《普通物理学》（第7版）课后习题答案解析

1-1 一质点沿Ox轴运动，坐标与时间的变化关系为x＝4t－2t³，式中x、t分别以m、s为单位，试计算：（1）在最初2s内的平均速度，2s末的瞬时速度；（2）1s末到3s末的位移、平均速度；（3）1s末到3s末的平均加速度；此平均加速度是否可用a—＝（a₁＋a₃）/2计算？（4）3s末的瞬时加速度。

解：本题考查了速度和加速度的定义以及平均速度、瞬时速度、平均加速度和瞬时加速度的计算。

由题意可知运动方程为x＝4t－2t³，可得瞬时速度为v＝dx/dt＝4－6t²，瞬时加速度为a＝dv/dt＝－12t。

（1）质点在最初2s内的平均速度为

v—＝（x₂－x₀）/Δt＝[（4×2－2×2³）－0]/（2－0）m/s＝－4m/s

其中“－”号表示平均速度的方向与Ox轴正方向相反（以下凡是出现“－”号均为此意）。

质点在2s末的瞬时速度为：

v₂＝（4－6t²）|_t＝2＝（4－6×2²）m/s＝－20m/s

（2）质点在1s末到3s末的位移为

Δx＝x₃－x₁＝[（4×3－2×3³）－（4×1－2×1³）]m＝－44m

质点在1s末到3s末的平均速度为

v—＝（x₃－x₁）/Δt＝（－42－2）/（3－1）m/s＝－22m/s

（3）质点在1s末到3s末的平均加速度为

a—＝（v₃－v₁）/Δt＝[（4－6×3²）－（4－6×1²）]/（3－1）m/s²＝－24m/s²

（4）质点在3s末的瞬时加速度为

a₃＝－12t|_t＝3＝－12×3m/s²＝－36m/s²

1-2 一质点沿Ox轴运动，其运动学方程为x＝5＋3t²－t³，式中x的单位为m，t的单位为s。

（1）试描述该质点的运动情况（在哪段时间内作加速运动？在哪段时间内作减速运动？在哪段时间内沿Ox轴正方向运动？在哪段时间内沿Ox轴负方向运动？）并画出x-t图、v-t图和a-t图。

（2）试求最初4s内质点的平均速度和平均速率。

解：本题考查了利用运动学方程求解运动学参数、利用图像对相关运动进行定量描述以及平均速度和平均速率的计算。

由题已知运动学方程为x＝5＋3t²－t³，分别求一阶导数和二阶导数，可得质点的速度和加速度分别为

v＝dx/dt＝6t-3t²，a＝dv/dt＝6-6t。

（1）分别作出x-t，v-t和a-t图像，如习题1-2图所示。

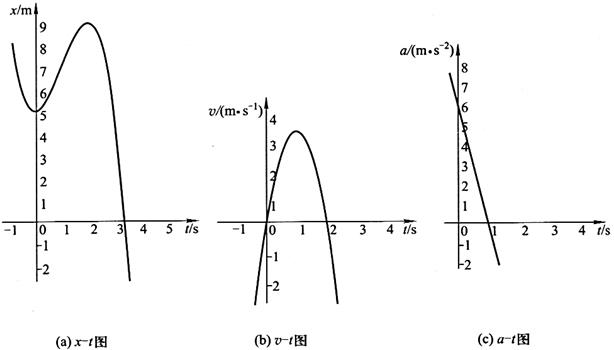
习题1-2图

由图可知，质点的运动分为以下几个阶段：

0s＜t＜1s：质点沿x轴正向作加速运动，速度逐渐增大，加速度逐渐减小但大于0。

t＝1s时，质点速度达到最大值，加速度减为0。

1s＜t＜2s：质点沿x轴正向作减速运动，速度逐渐减小，加速度小于0且逐渐增大。

t＝2s时，质点沿x轴正向的运动停止，速度减为0。

t＞2s：质点沿x轴负向作加速运动，速度逐渐增大，加速度逐渐增大。

（2）由质点的运动学方程可得0-4s质点的位移为x₄－x₁＝（－11）－5＝－16m，所以最初4s内质点的平均速度为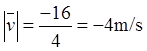

考虑到质点在前4s内的运动方向发生过变化，因此前4s内总的路程为s_0-4＝s_0-2＋s_2-4＝24m，所以最初4s内质点的平均速率为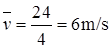

内容来源

程守洙《普通物理学》（第7版）考点笔记讲义

扫码阅读

1-3 已知质点的运动学方程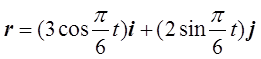
式中r的单位为m，t的单位为s。
（1）求质点的轨迹方程，并画出轨迹图。
（2）求t₁＝1s和t₂＝2s之间的，和的数值。
（3）求t₁＝1s和t₂＝2s两时刻的速度和加速度。
（4）在什么时刻质点的位矢与其速度矢量恰好垂直？求这时它的坐标。（提示：若两矢量和垂直，则）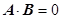
解：本题考查了利用运动学方程求解轨迹方程以及相关的运动学参数。
（1）由题可知质点在x和y方向的运动学方程分别为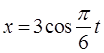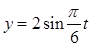，联立消去时间t，可得质点的轨迹方程为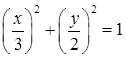，即其轨迹是一个椭圆，如下图所示

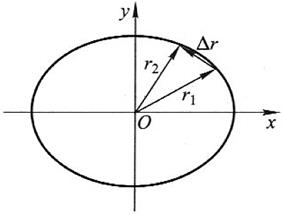
习题1-3图
（2）直接代入质点的运动学方程，可得1-2s内质点的位移为

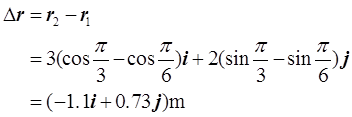
其与Ox轴正方向的夹角为

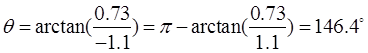
位移的大小为

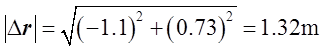
两个时刻位移大小的差值为

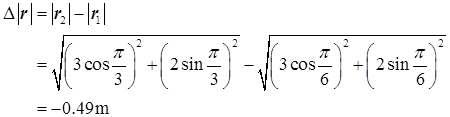
（3）对质点的运动学方程求一阶导数，可得质点在时刻t的速度为

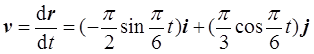
所以t₁＝1s时质点的速度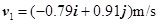为，其大小为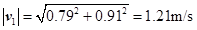，与Ox轴正方向的夹角为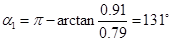
同理可得t₂＝2s时质点的速度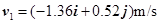为，其大小为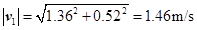，与Ox轴正方向的夹角为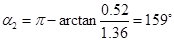
对速度表达式求一阶导数，可得质点在时刻t的加速度为

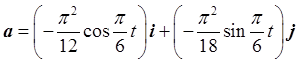
所以t₁＝1s时质点的加速度为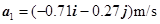，其大小为，与Ox轴正方向的夹角为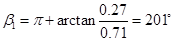
所以t₁＝2s时质点的加速度为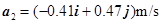，其大小为，与Ox轴正方向的夹角为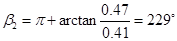
（4）当位矢与速度的点积为0时二者互相垂直，即

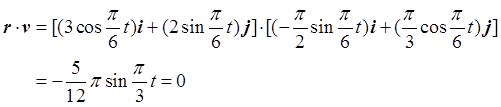
解得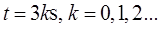
这些时刻对应椭圆上的坐标为（3，0），（0，2），（－3，0）和（0，－2）四个点。

1-4 一物体在黏性流体中沿直线运动，其加速度和速度的关系为a＝－kv²，式中k为正值常量，已知t＝0时，x＝0，v＝v₀，求该物体在任意时刻的速度和运动方程。
解：本题考查了利用积分法和已知运动学参数的关系求解其他运动学参数和运动方程。
由题可知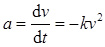，分离变量可得，对上式作定积分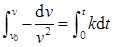，解得任意时刻t物体的速度为。
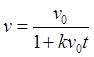改写速度表达式为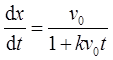，分离变量可得。
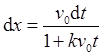同理作定积分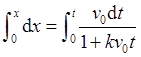，解得任意时刻t物体的运动方程为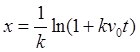
 
1-5 火箭沿垂直方向由静止向上发射，其加速度随时间的变化规律如习题1-5图所示，试求火箭在t＝50s时燃料用完那一瞬时所能到达的高度及该时刻的速度。

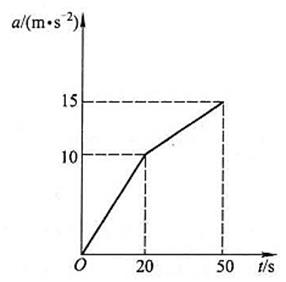
习题1-5图
解：本题考查了利用图像求解相关运动学参数。
在a-t图像中，曲线与x轴所围的面积即为速度的大小，因此由题可知t＝50s时火箭的速度为

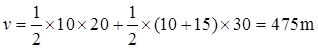
写出加速度的表达式为

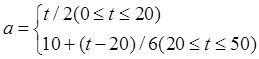
对其进行积分，并代入v_t＝20＝100m/s，可得速度表达式为

所以可得t＝50s时火箭到达的高度为

 
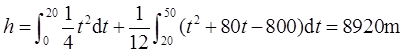
1-6 路灯距地面的高度为h，一个身高为l的人在路上匀速运动，速度为v₀，如习题1-6图所示，求：（1）人影中头顶的移动速度；（2）影子长度增长的速率。

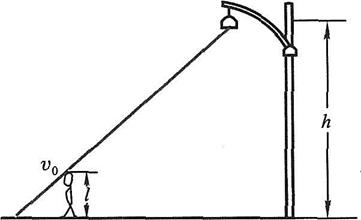
习题1-6图
解：本题考查了利用几何关系对运动参数的求解。
（1）如习题1-6解图所示，在地面建立向右为正方向的Ox坐标轴，易得路灯位于x_a＝a处，假设时刻为t的时候人的位置在x′处，人影的头顶点的位置在x处。
根据相似三角形的几何关系可得（a－x）/h＝（x′－x）/l，解得x＝（hx′－al）/（h－l）。
根据速度的定义式可得人影的头顶点运动的速度为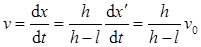（式中dx′/dt＝v₀为人的运动速度）。
因为h/（h－l）＞1，所以得出v＞v₀，即人影的头顶点移动的速度快于人。

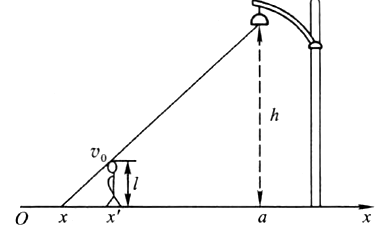
习题1-6解图
（2）由（1）可得人影的长度为x′－x＝x′－（hx′－al）/（h－l）＝（al－hx′）/（h－l）。
所以人影长度随时间的变化率为

上式表明，随着人接近路灯，人影长度将变短。
 
1-7 如习题1-7图所示，在离水面高度为h的岸边，有人用绳子拉船靠岸，船在离岸边s距离处，人收绳的速率为v₀。（1）从图中看出和各表示什么？（2）求船的速度与加速度各有多大。

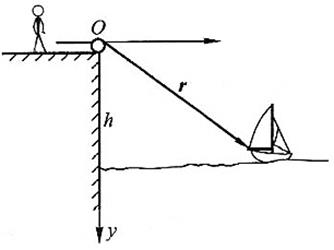
习题1-7图
解：本题考查了对关联运动的理解以及关联运动中速度和加速度的计算。
（1）由题图可知，r代表了由O指向船头的有向线段，因此表示了船头（船）的运动速度；同理，r表示了绳子到船头的距离，因此表示了绳子长短变化的快慢，即收绳的速率。
 
（2）建立Oxy坐标系如习题1-7解图所示，其中dr表示船头的位移，dr表示绳长的变化，二者夹角为θ。由题可知船到岸边的距离为s，水面离岸边的高度为h，所以有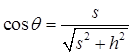，由图中几何关系可得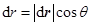，考虑到收绳速率为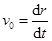，所以船的运动速度为

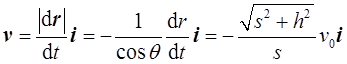
其大小为。
考虑到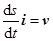，计算可得船的加速度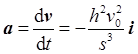为，其大小为。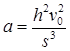

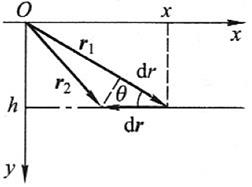
习题1-7解图

……

 完整版链接：/Ebook/994678.html

【目录】达聪学习网“程守洙《普通物理学》第七版复习笔记电子书”

  热门文章

——————————————————————————————

· 注册电气工程师供配电基础考试历年真题题库

· 张之恒中国考古通论教材课后习题集

· 陈先达马克思主义哲学原理第5版复习笔记电子书