陈敏恒化工原理第5版课后题答案

陈敏恒《化工原理》第三章课后习题答案节选

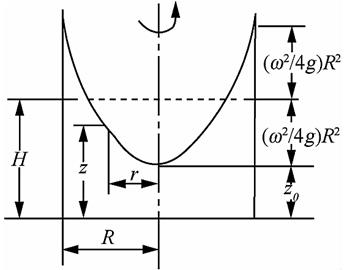
3-1 如图3-2-1所示，某搅拌器带动槽内全部液体以等角速度ω旋转，搅拌槽为敞口，中心处液面高度为z₀。试证：

图3-2-1

（1）半径为r处的液面高度满足

（2）设槽内液体静置时的液面高度为H，则

证明：（1）搅拌器带动槽内液体以等角速度ω旋转，液体中任一质点m（x，y，z）处的离心惯性力F＝mrω²。

单位质量离心力F/m在x轴、y轴方向的分量为

X＝rω²cosα＝xω²

Y＝rω²sinα＝yω²

沿z方向的质量力分量为Z＝－g，将单位质量力带入等压面微分方程式有

dp＝ρ（xω²dx＋yω²dy－gdz）＝0

积分有

x²ω²/2＋y²ω²/2－gz＝0

r²ω²/2－gz＝C

在自由表面上当r＝0，z＝0可得积分常数C＝0，故自由液面方程为

z＝ω²r²/（2g）

半径为r处的液面高度为

z＝z₀＋ω²r²/（2g）

（2）槽内液体在搅拌器的带动下液面呈抛物体状

V_拋＝πω²R⁴/（4g）①

液体体积不变

πR²H－V_拋＝πR²z₀②

联立①、②可得

z₀＝H－ω²R²/（4g）

搅拌功率

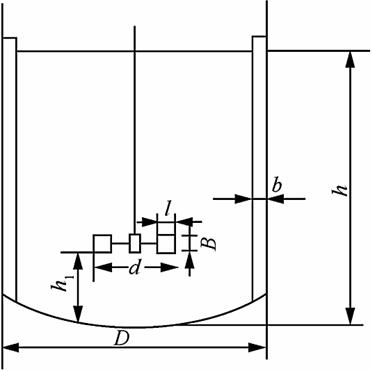
3-2 某开启式平直叶涡轮搅拌装置，D/d＝3，h₁/d＝1，d/B＝5（各符号命名参见图3-2-2）。搅拌槽内设有挡板，搅拌器有六个叶片，直径为150mm，转速为300r/min，液体密度为970kg/m³，黏度为1.2mPa·s，试估算搅拌器的功率。若上述搅拌装置中搅拌液体的黏度增加了10倍，密度基本不变，此时搅拌器的功率有何变化？

图3-2-2 典型的搅拌器各部比例

解：已知：涡轮叶片数Z＝6，D/d＝3，B/d＝1/5，l/d＝1/4，h₁/d＝1，ρ＝970㎏/m³，n＝300r/min，μ＝1.2mPa·s，d＝150mm。求：（1）P；（2）P′。

（1）雷诺数

Re＝ρnd²/μ＝970×300×0.15²/（1.2×10^－3×60）＝9.1×10⁴＞10⁴

此时液体为湍流状态，由教材图3-9曲线2查得K＝4.2，则

P＝Kρn³d⁵＝4.2×970×（300/60）³×0.15⁵＝38.7W

（2）当μ′＝（10＋1）μ＝11μ时，其他条件不变，有

Re′＝ρnd²/μ′＝ρnd²/（11μ）＝Re/11＝9.1×10⁴/11＝8.3×10³

由教材图3-9曲线2查得K′＝4.0，则

P′＝K′ρn³d⁵＝4.0×970×（300/60）³×0.15⁵＝36.8W

搅拌器放大

3-3 在小规模生产时搅拌某液体所用的搅拌釜容积为10L，采用直径为75mm开启平直叶涡轮搅拌器，在转速为1500r/min时获得良好的搅拌效果。试以单位体积搅拌功率相等为准则，计算1m³搅拌釜中搅拌器的直径、转速与功率的放大比值。

设两种情况下均在充分湍流区操作。

解：已知：V₁＝10L，V₂＝1m³，d₁＝75mm，r＝1500r/min。求：d₂/d₁，n₂/n₁，P₂/P₁。

（1）因为单位体积搅拌功率相等，所以V∝d³，得到V₂/V₁＝d₂³/d₁³，则

（2）又因为单位体积搅拌功率相等，可知n₁³d₁²＝n₂³d₂²，则

（3）又因为单位体积搅拌功率相等，即P₁/V₁＝P₂/V₂，则

P₂/P₁＝V₂/V₁＝1/0.01＝100

……

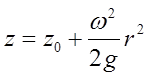
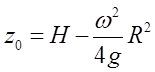
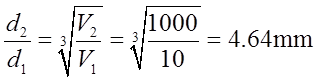
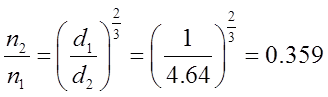
完整内容见达聪学习网“陈敏恒《化工原理》笔记和课后题答案解析”

  热门文章

——————————————————————————————

· 翻译专业资格考试英语三级笔译视频教程

· 2021年中国农业银行招聘考试历年真题答案详解

· CPA注册会计师财务成本管理章节考点题库