奥本海姆《信号与系统》（第2版）课后习题答案 【完整内容点击文中链接获取】
1-1 用笛卡儿坐标形式（x＋yj）表示下列复数。
ejπ/2，e－jπ/2，ejπ/2，e－jπ/2，ej5π/2，
，
，
，
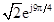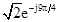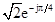
解：利用欧拉公式：
和复平面性质
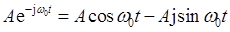
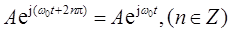
有：
ejπ/2＝（cosπ）/2＋（jsinπ）/2＝－1/2，e－jπ/2＝（cosπ）/2－（jsinπ）/2＝－1/2
ejπ/2＝cos（π/2）＋jsin（π/2）＝j，e－jπ/2＝cos（π/2）－jsin（π/2）＝－j
ej5π/2＝ejπ/2＝cos（π/2）＋jsin（π/2）＝j
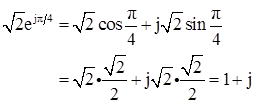
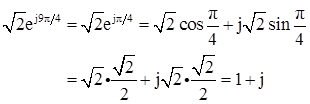
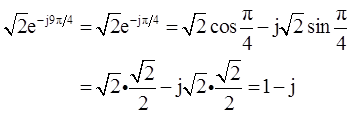
【总结】笛卡儿坐标形式（x＋yj）表示复数的时候，核心是找到对应的实部x和虚部y。大多数情况需要利用到欧拉公式ejθ＝cosθ＋jsinθ展开，另外虚指数信号具有周期性，也就是ejθ＝ej（θ±2mπ）＝cosθ＋jsinθ。
1-2 用极坐标形式（rejθ，－π＜θ≤π）表示下列复数。
5，－2，－3j，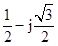
，1＋j，（1－j）2，j（1－j），（1＋j）/（1－j），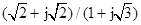
解：根据5，－2，－3j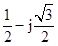，，1＋j，（1－j）2，j（1－j），（1＋j）/（1－j），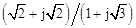
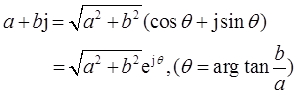
有：
5＝5cos0＋5jsin0＝5ej0
－2＝2cosπ＋2jsinπ＝ejπ
－3j＝3cos（－π/2）＋j3sin（－π/2）＝3e－jπ/2
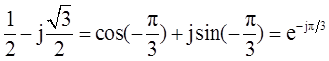
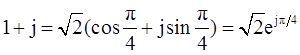
（1－j）2＝－2j＝2cos（－π/2）＋j2sin（－π/2）＝2e－jπ/2
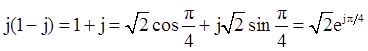
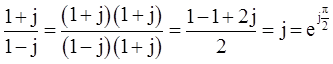
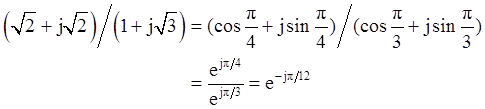
1-3 对下列每一个信号求P∞和E∞。
（a）x1（t）＝e－2tu（t）。
（b）x2（t）＝ej（2t＋π/4）。
（c）x3（t）＝cos（t）。
（d）x1[n]＝（1/2）nu[n]。
（e）x2[n]＝ej[π/（2n）＋π/8]。
（f）x3[n]＝cos（πn/4）。
解：（a）
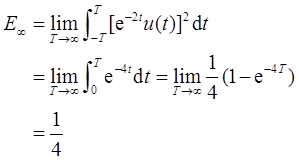
（b）
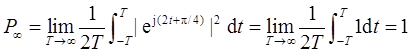
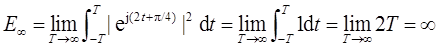
（c）
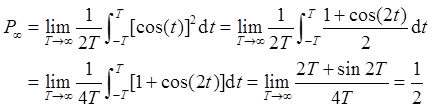
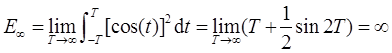
（d）
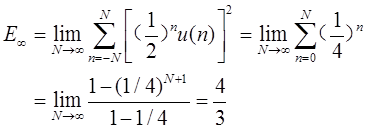
（e）
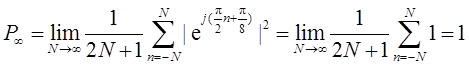
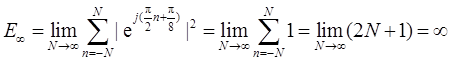
（f）
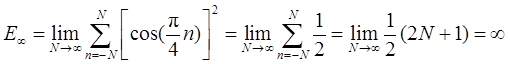
【总结】连续时间信号和离散时间信号的能量和功率的计算公式不一样。
对于连续时间信号：能量
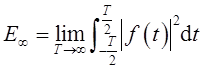
功率
对于离散时间信号：能量
功率
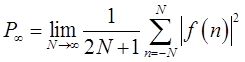
1-4 设n＜－2和n＞4时x[n]＝0，对以下每个信号确定其值保证为零的n值。
（a）x[n－3]。
（b）x[n＋4]。
（c）x[－n]。
（d）x[－n＋2]。
（e）x[－n－2]。
解：（a）x[n－3]＝0，（n－3）＜－2或（n－3）＞4，即x[n－3]＝0，n＜1或n＞7。
（b）x[n＋4]＝0，（n＋4）＜－2或n＋4＞4，即x[n＋4]＝0，n＜－6或n＞0。
（c）x[－n]＝0，（－n）＜－2或（－n）＞4，即x[－n]＝0，n＜－4或n＞2。
（d）x[－n＋2]＝0，（－n＋2）＜－2或（－n＋2）＞4，即x[－n＋2]＝0，n＜－2或n＞4。
（e）x[－n－2]＝0，（－n－2）＜－2或（－n－2）＞4，即x[－n－2]＝0，n＜－6或n＞0。
…………
【完整版】 达聪网 奥本海姆《信号与系统》（第2版）笔记和课后习题（含考研真题）详解
热门内容
