
《运筹学》第4版课后习题答案解析
第2章 线性规划与目标规划
2.1用图解法求解下列线性规划问题,并指出问题是具有惟一最优解、无穷多最优解、无界解还是无可行解?
(1)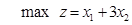

解:如图2-1所示,该问题的可行域为有界域。目标函数 在点A3处取得最大值,求解方程组
在点A3处取得最大值,求解方程组
 可得A3的坐标为(2,4),所以
可得A3的坐标为(2,4),所以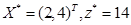 ,该线性规划问题具有惟一最优解。
,该线性规划问题具有惟一最优解。
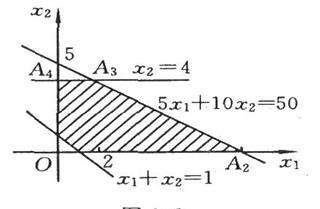
图2-1
(2)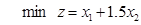
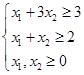
解:如图2-2所示,该线性规划问题的可行域无界。目标函数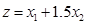 在点A处取得最小值,求解方程组
在点A处取得最小值,求解方程组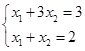 得A点的坐标为
得A点的坐标为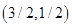 ,所以
,所以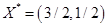 ,
,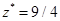 ,该问题具有惟一最优解。
,该问题具有惟一最优解。
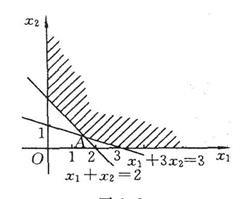
图2-2
(3)
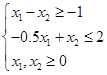
解:如图2-3所示,该问题的可行域无界。目标函数可以增加到无穷大,因此该问题具有无界解。
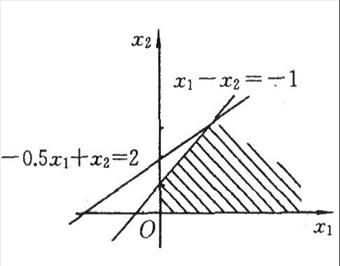
图2-3
(4)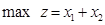
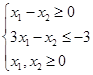
解:如图2-4所示,该问题的可行域为空集,因此该线性规划无可行解。
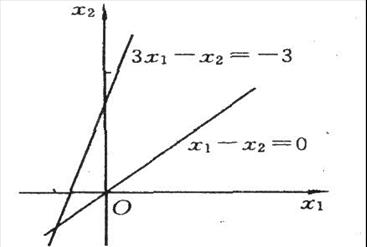
图2-4
2.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)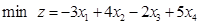
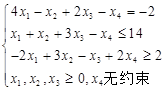
解:令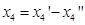 ,且
,且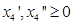 ;在第一个约束条件两边同时乘以-1后引入人工变量
;在第一个约束条件两边同时乘以-1后引入人工变量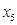 ,在第二个约束条件右端加上松弛变量
,在第二个约束条件右端加上松弛变量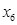 ;在第三个约束条件右端减去剩余变量
;在第三个约束条件右端减去剩余变量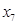 ,同时加入人工变量
,同时加入人工变量 ,将目标函数最小化变换为最大化,得该线性规划的标准型
,将目标函数最小化变换为最大化,得该线性规划的标准型

其中,M为充分大的正数,对应的初始单纯形表如表2-1所示:
表2-1

(2)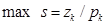
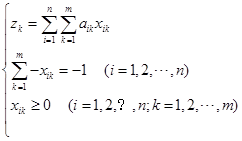
解:在上述约束条件两边同时乘以-1,然后分别引入人工变量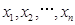 ,得该线性规划的标准型
,得该线性规划的标准型

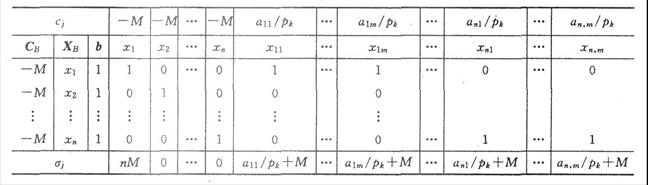
其中,M为充分大的正数。对应的初始单纯形表如表2-2所示:
表2-2
2.3在下面的线性规划问题中找出满足约束条件的所有基解,指出哪些是基可行解,并代入目标函数,确定哪一个是最优解。
(1)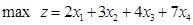
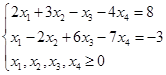
解:在第二个约束条件两边同时乘以-1,得到该线性规划问题的系数矩阵

①因为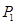 、
、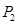 线性无关,故有
线性无关,故有
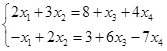
令非基变量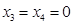 ,解得
,解得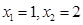 ,故有基可行解
,故有基可行解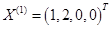 ,
,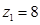 。
。
②因为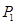 、
、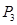 线性无关,故有
线性无关,故有

令非基变量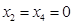 ,解得
,解得 ,故
,故 ,不是可行解。
,不是可行解。
③因为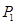 、
、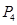 线性无关,故有
线性无关,故有
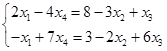
令非基变量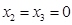 ,解得
,解得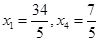 ,故有基可行解
,故有基可行解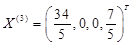 ,
,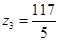 。
。
④因为 、
、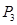 线性无关,故有
线性无关,故有
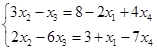
令非基变量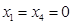 ,解得
,解得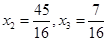 ,故有基可行解
,故有基可行解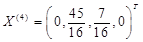 ,
,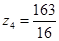 。
。
⑤因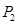 、
、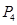 线性无关,故有
线性无关,故有

令非基变量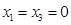 ,解得
,解得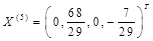 ,不是可行解。
,不是可行解。
⑥因 、
、 线性无关,故有
线性无关,故有
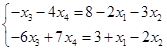
令非基变量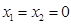 ,解得
,解得 ,不是可行解。
,不是可行解。
在 中,
中,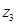 为最大值,所以最优解
为最大值,所以最优解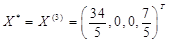 ,
, 。
。
(2)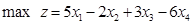
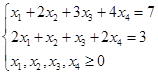
解:其系数矩阵为

①因为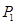 、
、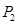 线性无关,故有
线性无关,故有
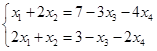
令非基变量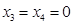 ,解得
,解得 ,不是可行解。
,不是可行解。
②因为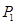 、
、 线性无关,故有
线性无关,故有
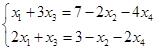
令非基变量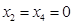 ,解得
,解得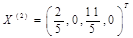 为基可行解,
为基可行解,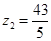 。
。
③因为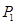 、
、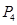 线性无关,故有
线性无关,故有
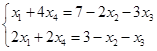
令非基变量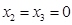 ,解得
,解得 ,不是可行解。
,不是可行解。
④因为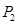 、
、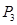 线性无关,故有
线性无关,故有

令非基变量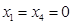 ,解得
,解得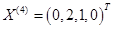 为基可行解,
为基可行解,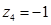 。
。
⑤因为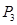 、
、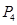 线性无关,故有
线性无关,故有
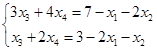
令非基变量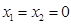 ,解得
,解得 为基可行解,
为基可行解,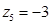 。
。
⑥因为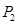 、
、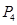 线性相关,故
线性相关,故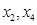 不能构成基变量。
不能构成基变量。
在 中,
中,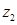 为最大值,所以最优解
为最大值,所以最优解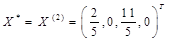 ,
,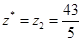 。
。
| 内容来源 |
《运筹学》第4版配套题库 |
扫码阅读 |
2.4用单纯形法求解习题2.1中的线性规划问题。
解(1)标准型为
max z=x1+3x2+0x3+0x4+0x5
s.t.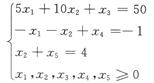
使用单纯形法求解,得到单纯形表:
表2-3
| cj | 1 | 3 | 0 | 0 | 0 | θi | ||
| CB | XB | b | x1 | x2 | x3 | x4 | x5 | |
| 0 | x3 | 50 | 5 | 10 | 1 | 0 | 0 | 5 |
| 0 | x4 | -1 | -1 | [-1] | 0 | 1 | 0 | 1 |
| 0 | x5 | 4 | 0 | 1 | 0 | 0 | 1 | 4 |

|
1 | 3 | 0 | 0 | 0 | |||
| 0 | x3 | 40 | -5 | 0 | 1 | 10 | 0 | 4 |
| 3 | x2 | 1 | 1 | 1 | 0 | -1 | 0 | - |
| 0 | x5 | 3 | -1 | 0 | 0 | [1] | 1 | 3 |

|
-2 | 0 | 0 | 3 | 0 | |||
| 0 | x3 | 10 | [5] | 0 | 1 | 0 | -10 | 2 |
| 3 | x2 | 4 | 0 | 1 | 0 | 0 | 1 | - |
| 0 | x4 | 3 | -1 | 0 | 0 | 1 | 1 | - |

|
1 | 0 | 0 | 0 | -3 | |||
| 1 | x1 | 2 | 1 | 0 | 1/5 | 0 | -2 | |
| 3 | x2 | 4 | 0 | 1 | 0 | 0 | 1 | |
| 0 | x4 | 5 | 0 | 0 | 1/5 | 1 | -1 | |

|
0 | 0 | -1/5 | 0 | -1 | |||
由表2-3得最优解X*=(2,4,0,5,0)T,max z=14。
(2)标准型为:
min z=x1+1.5x2+0x3+0x4+Mx5+Mx6,M为无穷大正数。
s.t.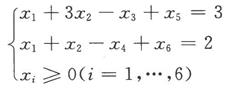
使用单纯形法求解,得到单纯形表,如表2-4所示。
表2-4
| cj | 1 | 1.5 | 0 | 0 | M | M | θi | ||
| CB | XB | b | x1 | x2 | x3 | x4 | x5 | x6 | |
| M | x5 | 3 | 1 | [3] | -1 | 0 | 1 | 0 | 1 |
| M | x6 | 2 | 1 | 1 | 0 | -1 | 0 | 1 | 2 |

|
-5M | 1-2M | 1.5-4M | M | M | 0 | 0 | ||
| 1.5 | x2 | 1 | 1/3 | 1 | -1/3 | 0 | 1/3 | 0 | 3 |
| M | x2 | 1 |
[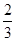 ] ]
|
0 | 1/3 | -1 | -1/3 | 1 | 3/2 |

|
-M-1.5 |
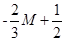
|
0 |
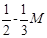
|
M |

|
0 | ||
| 1.5 | x2 | 1/2 | 0 | 1 | -1/2 | 1/2 | 1/2 | -1/2 | |
| 1 | x1 | 3/2 | 1 | 0 | 1/2 | -3/2 | -1/2 | 3/2 | |

|
-9/4 | 0 | 0 | 1/4 | 3/4 |
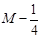
|
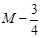
|
||
由表2-4得最优解X*=(3/2,1/2,0,0,0,0),min z=9/4。
(3)标准型为:
max z=2x1+2x2+0x3+0x4
s.t.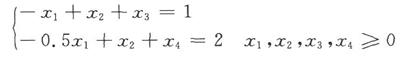
使用单纯形法求解,得到单纯形表如表2-5所示:
表2-5
| cj | 2 | 2 | 0 | 0 | θi | ||
| CB | XB | b | x1 | x2 | x3 | x4 | |
| 0 | x3 | 1 | -1 | [1] | 1 | 0 | 1 |
| 0 | x4 | 2 | -1/2 | 1 | 0 | 1 | 2 |

|
2 | 2 | 0 | 0 | |||
| 2 | x2 | 1 | -1 | 1 | 1 | 0 | - |
| 0 | x4 | 1 | [1/2] | 0 | -1 | 1 | 2 |

|
4 | 0 | -2 | 0 | |||
| 2 | x2 | 3 | 0 | 1 | -1 | 2 | - |
| 2 | x1 | 2 | 1 | 0 | -2 | 2 | - |

|
0 | 0 | 6 | -8 | |||
由表2-5可知,非基变量x3的检验数为6>0,但其系数均小于0,因此线性规划问题为无界解。
(4)标准型为:
max z=x1+x2+0x3+0x4
s.t.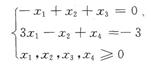
使用单纯形法求解,得到单纯形表:
表2-6
| cj | 1 | 1 | 0 | 0 | θi | ||
| CB | XB | b | x1 | x2 | x3 | x4 | |
| 0 | x3 | 0 | —1 | [1] | 1 | 0 | 0 |
| 0 | x4 | -3 | 3 | -1 | 0 | 1 | 3 |

|
0 | 1 | 1 | 0 | 0 | ||
| 1 | x2 | 0 | [-1] | 1 | 1 | 0 | 0 |
| 0 | x4 | -3 | 2 | 0 | 1 | 1 | - |

|
-1 | 2 | 0 | -1 | 0 | ||
| 1 | x1 | 0 | 1 | [-1] | -1 | 0 | 0 |
| 0 | x4 | -3 | 0 | 2 | 3 | 1 | - |

|
-1 | 0 | 2 | 1 | 0 | ||
| 1 | x2 | 0 | -1 | 1 | 1 | 0 | |
| 0 | x4 | -3 | 2 | 0 | 1 | 1 | |

|
-1 | 2 | 0 | -1 | 0 | ||
由表2-6可知,此线性规划问题无解。
2.5以

为例用图解法,具体说明当目标函数中变量的系数怎样改变时,使满足约束条件的可行域的每一个顶点,都有可能使目标函数值达到最优。
解:(1)当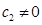 时,目标函数
时,目标函数 ,令
,令
①若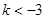 ,则当
,则当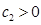 时,目标函数在点A3(4,0)处取得最大值;当
时,目标函数在点A3(4,0)处取得最大值;当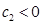 时,目标函数在原点(0,0)处取得最大值;
时,目标函数在原点(0,0)处取得最大值;
②若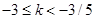 ,则当
,则当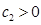 时,目标函数在点A2
时,目标函数在点A2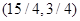 处取得最大值,其中
处取得最大值,其中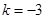 时,在线段A2A3上的任一点取得最大值;当
时,在线段A2A3上的任一点取得最大值;当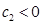 时,目标函数在原点处取得最大值;
时,目标函数在原点处取得最大值;
③若 ,则当
,则当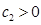 时,目标函数在点A1(0,3)处取得最大值,其中
时,目标函数在点A1(0,3)处取得最大值,其中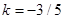 时,在线段A1A2上的任一点取得最大值;当
时,在线段A1A2上的任一点取得最大值;当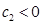 时,目标函数在坐标原点处取得最大值;
时,目标函数在坐标原点处取得最大值;
④若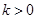 ,则当
,则当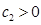 时,目标函数在点A1(0,3)处取得最大值;当
时,目标函数在点A1(0,3)处取得最大值;当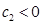 时,目标函数在点A3(4,0)处取得最大值。
时,目标函数在点A3(4,0)处取得最大值。
(2)当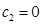 时,目标函数
时,目标函数
①当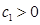 时,目标函数在点A3(4,0)处取得最大值;
时,目标函数在点A3(4,0)处取得最大值;
②当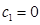 时,目标函数在可行域OA1A2A3中的任一点处均可取得最大值;
时,目标函数在可行域OA1A2A3中的任一点处均可取得最大值;
③当 时,目标函数在线段OA1上的任一点取得最大值。
时,目标函数在线段OA1上的任一点取得最大值。
【完整版】 达聪学习网 “《运筹学》第4版配套题库【名校考研真题+课后习题+章节题库+模拟试题】”
热门内容
——————————————————————————————







