曾谨言《量子力学教程》(第3版)笔记和课后习题(含考研真题)详解 【完整内容点链接获取】
立即获取: /Ebook/993285.html
第一章 波函数与Schrödinger方程
1-1 设质量为m的粒子在势场V(r)中运动。
(a)证明粒子的能量平均值为E=∫Wd3r,式中
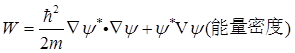
(b)证明能量守恒公式
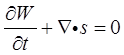
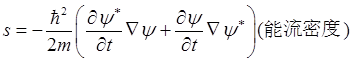
证明:(a)由力学量的平均值可得:粒子能量平均值为(设ψ已归一化)
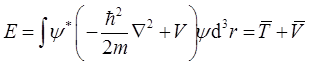
![]()
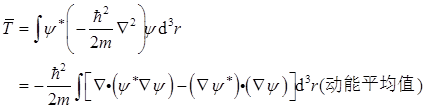
其中第一项可化为面积分,对于归一化的波函数,可以证明此面积分为零(见《量子力学教程》,18页脚注),所以
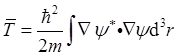
(b)按能量密度W和能流密度s的定义和含时薛定谔方程
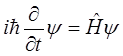
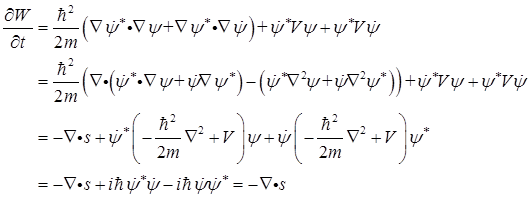
因此
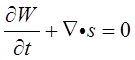
1-2 考虑单粒子的Schrodinger方程
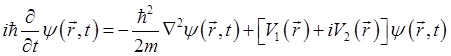
V1与V2为实函数。
(a)证明粒子的概率(粒子数)不守恒。
(b)证明粒子在空间体积τ内的概率随时间的变化为
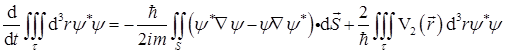
证明:由已知Schrodinger方程
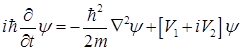 ①
①
取复共轭
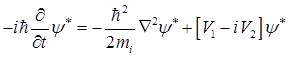 ②
②
①×ψ*-②×ψ得
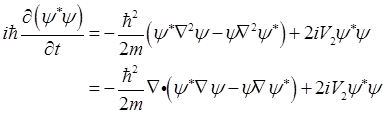
利用Stokes定理将体积分转化为面积分,可得
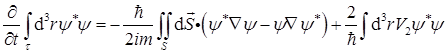
对于可归一化波函数,当τ→∞,上式第一项(面积分)为0,而V2≠0,所以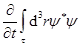 不为0,即粒子数不守恒。
不为0,即粒子数不守恒。
1-3 对于一维自由粒子
(a)设波函数为
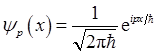
试用Hamilton算符
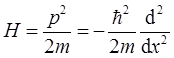
对ψp(x)运算,验证
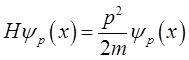
说明动量本征态ψp(x)是Hamilton量(能量)本征态,能量本征值为E=p2/(2m)
(b)设粒子在初始(t=0)时刻,ψ(x,0)=ψp(x),求ψ(x,t)
(c)设波函数为
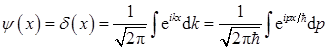
可以看成无穷多个平面波eikx的叠加,即无穷多个动量本征态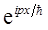 的叠加,试问ψ(x)=δ(x)是否是能量本征态?
的叠加,试问ψ(x)=δ(x)是否是能量本征态?
(d)设粒子在t=0时刻ψ(x,0)=δ(x),求ψ(x,t)。
解:(a)利用已知条件带入可得
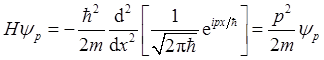
所以动量本征态ψp(x)是Hamilton量(能量)的本征态,能量本征值为E=p2/(2m)。
(b)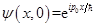 其Fourier变换为
其Fourier变换为
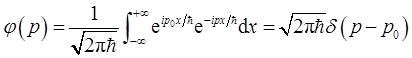
由于ψ(x,0)是能量本征态,因此,
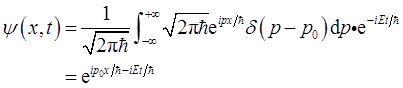
(c)对于自由粒子,动量本征态,亦即能量本征态,由于δ(x)是无穷多个动量本征态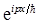 的叠加,所以ψ(x)=δ(x)不是动量本征态,即可以推知它也不是能量本征态。
的叠加,所以ψ(x)=δ(x)不是动量本征态,即可以推知它也不是能量本征态。
(d)因为ψ(x,0)=δ(x),由傅里叶变换可得:
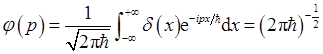
所以

计算中利用了积分公式
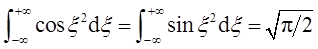
或
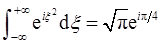
所以
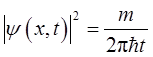
……
【完整版】 达聪网 曾谨言《量子力学教程》(第3版)笔记和课后习题(含考研真题)详解
热门内容






